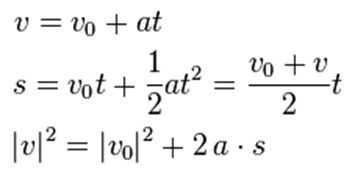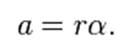ACCELERATION
شتاب ( ACCELERATION )
شتاب، در فیزیک، به معنی نرخ تغییر سرعت در یک جسم است.
بر اساس قانون دوم نیوتن، شتاب یک جسم، برآیند خالص تمامی نیروهایی است که بر جسم اعمال می شوند. واحد SI برای شتاب، متر بر مجذور ثانیه است (m/s2). شتاب ها مقادیر برداری هستند (که اندازه و جهت دارند) و بر اساس قانون متوازی الاضلاع با یکدیگر جمع می شوند.
به عنوان یک بردار، نیروی خالص محاسبه شده، برابر با حاصلضرب جرم جسم (یک کمیت اسکالر) در شتاب آن جسم است.
برای مثال، هنگامی که یک اتومبیل از حالت ایستا (سرعت نسبی صفر) شروع به حرکت کرده و در یک خط مستقیم با سرعتی رو به افزایش حرکت می کند، در مسیر حرکت خود شتاب می گیرد.
اگر اتومبیل تغییر جهت دهد، آنگاه در آن مسیر جدید شتاب می گیرد.
برای مثال، ما می توانیم شتاب افزایشی یک اتومبیل در مسیر پیشرونده (حرکت رو به جلو) را بعنوان “شتاب خطی” نامگذاری کنیم، که مسافران در یک اتومبیل، می توانند این شتاب را بصورت نیرویی که آنها را به سمت صندلی هایشان هل می دهد، تجربه کنند.
اگر تغییر جهت داشته باشیم، آن را با عبارت “شتاب غیر خطی” معرفی می کنیم، که مسافران آن را در قالب یک نیروی جانبی تجربه می کنند. اگر سرعت اتومبیل کاهش یابد، این یک شتاب در جهت عکس حرکت اتومبیل است، که گاهی با عبارت “شتاب منفی” نیز معرفی می شود.
مسافران می توانند این شتاب منفی را بصورت نیرویی که آنها را از صندلی بلند کرده و از آن دور می کند تجربه کنند. از نظر ریاضی، هیچ فرمول جداگانه ای برای کاهش سرعت (شتاب منفی) وجود ندارد، زیرا هر دوی آنها نوعی تغییر در سرعت هستند ( هم سرعت افزایشی و هم سرعت کاهشی نشانه نوعی تغییر در سرعت است).
هر یک از این شتاب ها (شتاب خطی، شتاب غیر خطی، شتاب کاهشی)، تا مادامی که سرعت آنها (سرعت و جهت مسافران) با سرعت اتومبیل یکی و سازگار نشده است، می تواند توسط مسافران احساس شود.
تعاریف و خصوصیات ACCELERATION
شتاب متوسط
مقدار میانگین شتاب ACCELERATION جسم در طی یک دوره زمانی، از تقسیم تغییرات سرعت آن جسم (Δν) بر طول دوره زمانی (tΔ) بدست می آید. بصورت ریاضی داریم:

شتاب لحظه ای
در ضمن، شتاب لحظه ای، از حد شتاب متوسط در طی یک فاصله زمانی بینهایت کوچک بدست می آید.
از نظر حساب انتگرال، شتاب لحظه ای، مشتق بردار سرعت نسبت به زمان است:
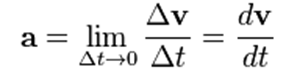
(در اینجا و جاهای دیگر، اگر حرکت در یک خط مستقیم باشد، می توان در معادلات، مقادیر برداری را با اسکالرها جایگزین نمود.)
می توان مشاهده نمود که انتگرال تابع شتاب (t)a، تابع سرعت (t)ν است؛ که در واقع سطح زیر منحنی شتاب- زمان است. نمودار مربوط به سرعت است.
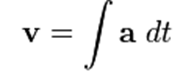
با توجه به این واقعیت که تعریف شتاب، مشتق سرعت V ، نسبت به زمان t و تعریف سرعت، مشتق مکان نسبت به زمان t است، شتاب می تواند از مشتق دوم مکان نسبت به زمان بدست آید:
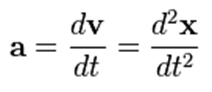
واحدها
واحد شتاب ACCELERATION همان بعد سرعت (L/T) تقسیم بر زمان است، برای مثال، L/T2. واحد شتاب در SI ،متر بر مجذور ثانیه (/S2M) است:
این می تواند معنی دار تر باشد اگر بگوییم: “متر بر ثانیه در هر ثانیه”، زیرا سرعت در متر بر ثانیه، در هر ثانیه، با مقدار شتاب تغییر می کند.
فرم ها و اشکال دیگر
جسمی که در حال حرکت در یک مسیر دایروی است،
مانند یک ماهواره که در مدار زمین حرکت می کند، به دلیل تغییر در جهت حرکت، سرعتی افزایشی دارد، اگرچه اندازه (سرعت) ممکن است ثابت باشد.
وقتی که جسمی بگونه ای حرکت کند که تغییر جهت داشته باشد اما سرعت آن تغییر نکند،
گفته می شود که تحت شتاب مرکز گرا (متمایل به سمت مرکز) قرار گرفته است.
در مقابل، اگر جسمی تغییر سرعت داشته باشد اما جهت حرکت آن تغییر نکند، به آن شتاب مماسی گفته می شود.
شتاب مناسب، یعنی شتاب ACCELERATION یک جسم نسبت به شرایط سقوط آزاد،
توسط وسیله ای به نام شتاب سنج اندازه گیری می شود.
در مکانیک کلاسیک، برای یک جسم با جرم ثابت،
(بردار) شتاب مرکز جرم یک جسم، با بردار نیروی خالص اعمال شده بر آن جسم (برای مثال، مجموع تمام نیروها) متناسب است (قانون دوم نیوتن):
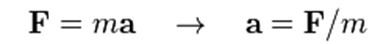
که در آن F نیروی خالص وارد برجسم، m جرم جسم و a شتاب مرکز جرم جسم است.
هرچه مقدار سرعت به سرعت نور نزدیک می شود، اثرات نسبیتی به طور فزاینده ای بزرگ شده و شتاب کمتر می شود.
شتاب مماسی و شتاب مرکز گرا
سرعت ACCELERATION یک ذره که در حال حرکت در یک مسیر منحنی است، می تواند بعنوان تابعی از زمان بصورت زیر نوشتهشود:
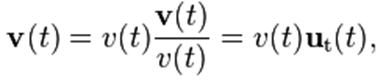
همراه با (t)ν که برابر با سرعت حرکت جسم در طول مسیر است و :
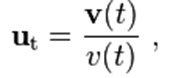
یک بردار واحد که منطبق بر مسیر حرکت است، به جهت حرکت در لحظه مورد نظر اشاره دارد.
با در نظر گرفتن سرعت متغیر (t)ν و تغییر جهت UT، شتاب یک ذره در حال حرکت در یک مسیر منحنی را می توان با استفاده از قاعده زنجیره ای تمایز برای حاصلضرب دو تابع زمانی، بصورت زیر نوشت :
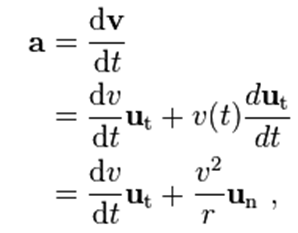
که در آن Un، بردار نرمال واحد (به سمت داخل) نسبت به مسیر حرکت ذره است (که به نام اصل نرمال معرفی شده) و r، شعاع انحنای آن در لحظه ای است که (در زمان t) با دایره تماس داشته است.
این مولفه ها، با نام شتاب مماسی و شتاب نرمال یا شتاب شعاعی نامیده می شوند (یا شتاب مایل به مرکز (مرکز گرا) در حرکت دایره ای. حرکت دایره ای و نیروی مرکز گرا را نیز ببینید).
تجزیه و تحلیل هندسی منحنی های فضایی سه بعدی، که خط مماس، (اصلی) نرمال و بینرمال (یک عبارت جبری که از مجموع یا تفاوت دو بردار حاصل می شود) را توضیح می دهند، توسط فرمول Frenet Serret تشریح می شود.
موارد خاص
شتاب یکنواخت
شتاب یکنواخت یا ثابت، نوعی حرکت است که در آن، سرعت یک جسم، در هر دوره زمانی، به یک اندازه تغییر می کند.
مثالی که مکررا برای تشریح شتاب یکنواخت به آن اشاره شده، جسمی است که در حال سقوط آزاد در یک میدان گرانشی یکنواخت است.
شتاب یک جسم در حال سقوط، در نبود مقاومت نسبت به حرکت، فقط به قدرت میدان گرانشی g ( که شتاب ناشی از گرانش نیز نامیده می شود) وابسته است.
بر اساس قانون دوم نیوتن، نیروی F وارد شده بر جسم، بصورت زیر است:
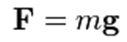
با توجه به خصوصیات جبری ساده شتاب ثابت در حالت تک بعدی (که شتابی در راستای سرعت اولیه است) فرمولهای ساده ای وجود دارد که به مقادیر جابجایی S، سرعت اولیه V0، سرعت نهایی V ، شتاب a و زمان t مربوط می شود.
که در آن :
S = مقادیر جابجایی
V0 = سرعت اولیه
V = سرعت نهایی
a = شتاب
t = زمان
زمانی که جسمی با شتاب یکنواخت، در ابتدای حرکت در مسیری قرار دارد که با راستای شتاب هم جهت نیست، این حرکت می تواند در دو بخش متعامد حل و فصل شود، یکی در سرعت ثابت و دیگری با توجه به معادله بالا.
همانطور که گالیله نشان داد، نتیجه خالص، یک حرکت سهموی است، زیرا در مسیر یک گلوله توپ، از مقاومت هوا صرف نظر می شود.
حرکت دایره ای
حرکت دایره ای یکنواخت که دارای سرعتی ثابت در امتداد یک مسیر دایره ای است، می تواند مثالی از شتاب جسمی باشد که در آن، اندازه سرعت ثابت ولی جهت حرکت متغییر است.
در این مورد، چون جهت حرکت جسم همواره در حال تغییر بوده و در تماس با دایره است، بردار سرعت خطی جسم نیز تغییر می کند، اما سرعت آن تغییر نمی کند.
این شتاب یک شتاب شعاعی است زیرا همیشه به سمت مرکز دایره متمایل بوده و مقدار آن برابر با رابطه زیر است :
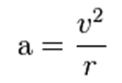
که در آن، پارامتر v، سرعت خطی جسم در راستای مسیر دایره ای است. بطور مشابه، می توان بردار شتاب شعاعی a را از سرعت زاویه ای جسم ω نیز بدست آورد.
که در آن، r برداری است که جهت آن همواره رو به بیرون دایره بوده و اندازه آن برابر با مقدار شعاع است.
علامت منفی فورمول بالا نشان می دهد که جهت بردار شتاب همواره متوجه مرکز دایره است (خلاف جهت شعاع).
شتاب و نیروی خالص اعمال شده بر جسم، در حرکت دایره ای یکنواخت، به سمت مرکز دایره جهت گیری دارد؛ برای همین، مرکز گرا و متمایل به مرکز است.
در حالی که اصطلاح “نیروی گریز از مرکز” که ظاهرا نیروی اعمال شده بر جسم با جهت گیری به سمت بیرون است، در واقع، یک شبه نیرو می باشد که با توجه به مومنتوم خطی جسم در نقطه ای منطبق بر دایره، در چارچوب مرجع جسم در حرکت دایره ای تجربه می شود.
با حرکت دایره ای غیر یکنواخت، برای مثال، سرعت در امتداد تغییرات مسیر منحنی، یک شتاب عرضی، برابر با نرخ تغییرات سرعت زاویه ای ، در پیرامون زمانهای دایره ای شعاع دایره ایجاد می شود. که داریم:
جهت گیری شتاب عرضی (یا مماسی) در مسیر دایره ای به نحوی است که با بردار شعاع، زوایای قائمه داشته باشد و دارای علامت شتاب زاویه ای است ( α).
ارتباط با نسبیت
نسبیت خاص
نظریه نسبیت خاص ، رفتار اجسامی را توصیف می کند که نسبت به اجسام دیگر با سرعت های بسیار زیاد (نزدیک به سرعت نور در خلا) حرکت می کنند. مکانیک نیوتنی تقریب نسبتا دقیقی از واقعیت است و با دقت زیادی که دارد، در سرعت های پایین تر نیز معتبر است.
هرچه مقدار سرعت های وابسته، نسبت به سرعت نور بیشتر شود، دیگر شتاب از معادلات کلاسیک تبعیت نخواهد کرد.
هرچه سرعت به مقدار سرعت نور نزدیک تر شود، شتاب ایجاد شده توسط یک نیرو کاهش خواهد یافت، بطوری که با نزدیک شدن به سرعت نور، بی نهایت کوچک می شود؛ یک جسم با یک مقدار جرم می تواند به طور مجانبی به این سرعت نزدیک شود، اما هرگز به آن نمی رسد.
نسبیت عام
کاملا غیر ممکن است که بتوان تشخیص داد آیا نیروی مشاهده شده، ناشی از گرانش است یا شتاب- گرانش، مگر آنکه حالت حرکت یک جسم شناخته شده باشد، شتاب اینرسیایی اثرات مشابه دارد.
آلبرت انیشتین این اصل را اصل هم ارزی می نامد و بر این عقیده است که فقط ناظرانی که هیچ نیروی احساس نمی کنند، از جمله نیروی گرانش، در رسیدن به این نتیجه که آنها در حال شتاب گرفتن نیستند، توجیه می شوند.
تبدیل ها
تبدیل های بین واحد های متداول شتاب
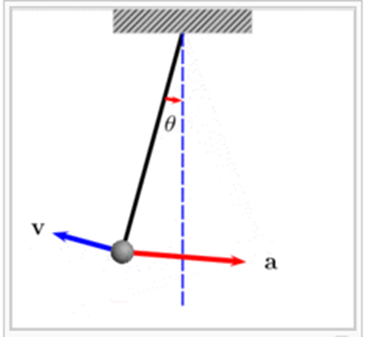
یک آونگ نوسانی، با سرعت و شتاب مشخص شده و هر دوی این شتاب ها ، شتاب مماسی و مایل به مرکز، را تجربه می کند.
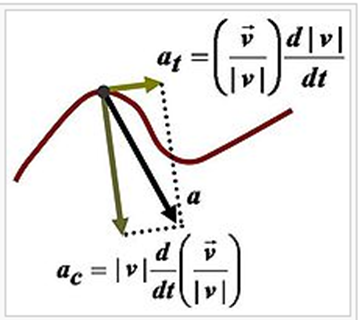
مولفه های شتاب یک حرکت منحنی.
مولفه مماسی at ، ناشی از تغییرات در سرعت پیمایشی و نقاط امتداد منحنی،
که در جهت بردار سرعت اند (یا در جهت مخالف) می باشد.
مولفه قائم ( که در حرکت دایره ای، مولفه مایل به مرکز نیز نامیده می شود)، ac ، ناشی از تغییر در جهت بردار سرعت است و عمود بر مسیر حرکت و جهت آن متوجه مرکز دایره است.
ترجمه و بازنویسی تیم مهندسی الکترومارکت.
منبع انگلیسی: https://en.wikipedia.org/wiki/Acceleration